Permutation and combinations are a part of core counting problem in mathematics. In biology also we encounter multiple situations where knowledge of permutations and combinations are handy. Here is a brief introduction to these concepts with the focus on biological problems.
1. Permutation
This is sampling problem where the position of items is significant. For example: a DNA sequence of certain length like ATT CGA AAT is a set of 9 nucleotide from a set of four: A T C G. So, how many possible DNA sequences of length 9 are possible? Lets review some concepts:
1.1 Permutation where repetition is allowed:
This is the most straight forward situation to understand. Lets say we need to get a subset of 3 items (k) from a nucleotide set of containing 4 items (n) . \(Nucleotide = \{A,T,C,G\}\). Then, each position has n possible options.
This can be written more concisely as:
\[\text{Permutation with repetition} = n^k\]Where:
n = total number of items in a set
k = number of items in the subset (this can be greater than n as well)
Now, coming back to the question about DNA sequence of length 9, there are \(9^4=6561\) possible DNA sequences.
1.2 Permutations without repetition
In many situations, like how many ways 10 athletes can be arranged in 1st, 2nd and 3rd position. Same athlete can not come in both 1st or other positions. So in this situation, 1st position has n options but second has n-1 and third has n-2 possibilities.
\(\text{Permutation without repetition} = \frac{n}{}.\frac{n-1}{}.\frac{n-2}{}....\frac{n-k}{}\)
Mathematically, this is written using factorial
It is important to note that subset here cannot be greater than the set itself. Therefore, in the example of athletes, there are \(\frac{10!}{(10-3)!}=720\)
2. Combination
This is a sampling problem where the position is not significant. We can sample k items from a set of n items with repetition or without repetition.
2.1 Combination without repetition
This can be taken as a special case of permutation without repetition, where subset with same items irrespective of their position is same. For example {1,2,3}, {1,3,2}, {2,1,3} are all same as {1,2,3}. Therefore we need to adjust the formula for permutation as follows:
\(\text{Combination without repetition} = \frac{n!}{(k!)(n-k)!}\) In R this can be calculated using choose function.
#Find possible combinations of 3 items from set of 5
choose(5,3)
## [1] 10
#To see all possible combinations
combn(1:5, 3)
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 1 1 1 1 1 1 2 2 2 3
## [2,] 2 2 2 3 3 4 3 3 4 4
## [3,] 3 4 5 4 5 5 4 5 5 5
In R to get the number of permutation, we can multiply the result of choose function with \(k!\).
#find possible permutation without repetition in R when 3 selected from 5
choose(5,3)*factorial(3)
## [1] 60
# when repetition is allowed
5^3
## [1] 125
Application of combination
One of the most popular application of combination is in binomial equation.
\[P(Y=k)= {n \choose k}p^k(1-p)^{n-k}\]In this equation \(n \choose k\) represents the possible ways by which k success can occur when the trial is repeated n times.
- Another application is when we need to calculate the number of pairwise list of genes from a set of genes. If there are 10 genes are we need to calculate the pairwise correlation between all possible pairs then it is given by :
\(_{10}C_{2}= {10 \choose 2}\) which is equal to 45.
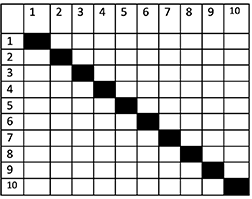
Fig: Pairwise combination of 10 items.
Lets look at this pairwise combination in more detail. There are \(10^2=100\) permutation possible with repetition, which represents all 100 squares in figure above. The combination which gives 45 represents only one half of the diagonal (either upper or lower). This number (45) is also equal to the number of possible paths in a non-directed network with 10 nodes. And if the network is directed then permutation without repetition can be used which will give 90 possible paths in that network, which is the number of all squares except diagonal.